Stock Analysis with AutoML

작성일 | In |

결과

내용을 작성하기에 앞서 결과적으로는 좋은 성능의 예측 모델을 만들지 못했다.

chart1

AutoML을 사용해 다양한 Feature(장 초반 생성되는 패턴)를 학습시켜 장 마감 지수를 예측하려고 했지만, 거의 예측을 하지 못하는 모델이 학습됐다.

접근

보통 시계열이나 회귀 문제로 접근하는 주식 시장의 흐름을 패턴에 맞춰 대응한다는 개념으로 분류 문제로 접근해보기로 했다.

현재 분석 가능한 데이터는 다음과 같다.

  • 거래소_선물지수 1분봉
  • 외국인거래소_매도금액 1분봉
  • 외국인거래소_매수금액 1분봉
  • 외국인거래소_선물매도량 1분봉
  • 외국인거래소_선물매수량 1분봉

위 목록의 데이터들은 2017년 1월부터 2021년 3월 초의 장 시작부터 장 마감까지 시가, 고가, 저가, 종가로 이루어져있다.

거래소_선물지수_1분봉.csv

1
2
3
4
5
6
7
8
9
10
11
12
13
14

            Date   Time    Open    High     Low   Close   Up  Down
0       20170102  10:01  260.05  260.30  260.00  260.10  409  1312
1       20170102  10:02  260.10  260.20  259.90  259.95  341   679
2       20170102  10:03  259.95  260.05  259.90  259.95  419   455
3       20170102  10:04  259.95  260.00  259.90  259.95  153   294
4       20170102  10:05  259.90  259.95  259.85  259.90  155   515
...          ...    ...     ...     ...     ...     ...  ...   ...
374322  20210305  15:32  411.90  412.20  411.90  412.10  455   194
374323  20210305  15:33  412.10  412.20  412.05  412.15  224   121
374324  20210305  15:34  412.15  412.25  412.05  412.05  214   266
374325  20210305  15:35  412.00  412.05  411.80  411.90  293   461
374326  20210305  15:46  411.75  411.75  411.75  411.75    0  4455
[374327 rows x 8 columns]

외국인거래소_매수금액_1분봉

1
2
3
4
5
6
7
8
9
10
11
12
13
14
             Date   Time      Open      High       Low     Close  Up  Down
0       20170102  08:31      0.00      0.00      0.00      0.00   0     0
1       20170102  08:32      0.00      0.00      0.00      0.00   0     0
2       20170102  08:34      0.00      0.00      0.00      0.00   0     0
3       20170102  08:35      0.07      0.07      0.07      0.07   0     0
4       20170102  08:37      0.07      0.07      0.07      0.07   0     0
...          ...    ...       ...       ...       ...       ...  ..   ...
414042  20210305  17:59  31984.56  31984.56  31984.56  31984.56   0     0
414043  20210305  18:01  31984.56  31984.56  31984.56  31984.56   0     0
414044  20210305  18:02  31984.69  31984.69  31984.69  31984.69   0     0
414045  20210305  18:04  31984.69  31984.69  31984.69  31984.69   0     0
414046  20210305  18:05  33121.43  33121.43  33121.43  33121.43   0     0

[414047 rows x 8 columns]

각 컬럼 "Date","Time","Open","High","Low","Close","Up","Down"는 날짜,시간,시가,고가,저가,종가,상승체결,하락체결을 의미한다.

모든 데이터들은 1분봉으로 이루어져 있기 때문에 시가, 고가 등등 1분동안 크게 변화가 없으므로 시가 정보인 Open 데이터만 분석에 사용한다.

거래소 선물지수 데이터는 그대로 사용하고 외국인 거래량, 거래액은 거래량을 사용하되 순 거래량을 계산해서 사용하기로 한다.

선물지수, 순거래량 차트

chart1
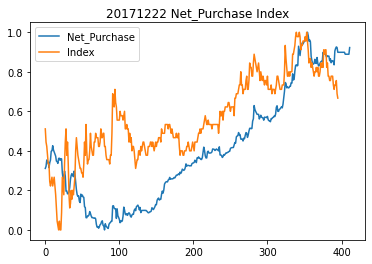
chart2
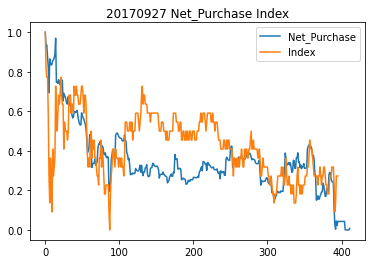
chart3

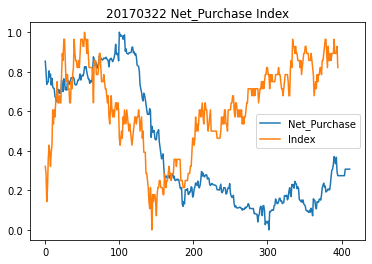
Net_Purchase는 외국인 순 거래량, Index는 선물지수이다.

데이터 처리

전체 데이터 중 일부 데이터를 사용해 두 지수를 비교하였고 값의 단위가 다르기 때문에 sklearn.preprocessing의 MinMaxScaler를 사용해 정규화를 진행했다.

두 데이터에서 학습 데이터를 추출해야 하는데 위에서 말했던 것 처럼 분류의 형태로 접근할 것이다.

장 초반에 생성되는 지수 패턴과 순매수량 패턴을 feature로 잡고 장 마감시 지수가 패턴이 끝날 때 지수보다 1%이상 상승했으면 Positive, 아니라면 Negative로 보고 이항 분류 형태의 데이터를 만들 것이다.

get_train_data

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
def get_train_data(pattern_data, index_data, 
                   target_pattern_column='Net_Purchase', target_index_column='Open',
                   use_index_data_to_pattern=False, need_increase_percentage=3,
                   pattern_start_position=0, pattern_end_position=30):
    

    dates = np.unique(pattern_data['Date'].values)
    feature_labels = []

    
    for date in dates:
        try:
            target_pattern_data = pattern_data[pattern_data['Date'] == date].iloc[:, 2:]
            target_index_data = index_data[pattern_data['Date'] == date].iloc[:, 2:]

            target_pattern_column_position = target_pattern_data.columns.get_loc(target_pattern_column)
            target_index_column_position = target_index_data.columns.get_loc(target_index_column)

            start_index_position = 0
            if use_index_data_to_pattern:
                start_index_position = pattern_end_position
            
            start_index = target_index_data[target_index_column].iloc[start_index_position]
            end_index = target_index_data[target_index_column].iloc[-1]
   
            label = 0
            if end_index >= (start_index + (start_index * 0.01 * need_increase_percentage)):
                label = 1

            scaler = MinMaxScaler()
            scaler.fit(target_pattern_data)
            scaled_target_pattern = scaler.transform(target_pattern_data)

            scaler = MinMaxScaler()
            scaler.fit(target_index_data)
            scaled_target_index = scaler.transform(target_index_data)

            feature_label = []
            
            for row in scaled_target_pattern[:, target_pattern_column_position][pattern_start_position:pattern_end_position]:
                feature_label.append(row)
                

            if use_index_data_to_pattern:
                for row in scaled_target_index[:, target_index_column_position][pattern_start_position:pattern_end_position]:
                    feature_label.append(row)

            feature_label.append(label)
            feature_labels.append(feature_label)

        except Exception as e:
            print('error in ' + date)
            print(e)

    return feature_labels

하루에 생성되는 데이터를 결합하여 한 row로 생성할 것이고 pattern_end_position부터 pattern_end_position 까지 생성되는 데이터를 패턴으로 판단하여 feature로 row에 추가한다.

기본값이 0 ~ 30으로 잡혀있는데 이는 장 시작 9:00 부터 장 마감 16:20 까지 420여개(종종 몇개의 분봉은 넘어가는 데이터도 존재함)의 분봉이 존재하므로 position값 1당 1분으로 봐도 무방하다.

즉 장 시작 30분간의 패턴을 학습에 사용되는 Feature로 사용한다는 뜻이다.

그 다음 장 마감시 지수가 장 초반 (패턴을 읽은 뒤 : 장 시작 30분 후) 지수보다 1%이상 상승했다면 Positive(1)로 아니라면 Negative(0)로 잡고 Label을 생성한다.

1
2
3
4
5
6
start_index = target_index_data[target_index_column].iloc[start_index_position]
end_index = target_index_data[target_index_column].iloc[-1]

label = 0
if end_index >= (start_index + (start_index * 0.01 * need_increase_percentage)):
    label = 1

마지막으로 모든 데이터를 MinMaxScaler로 정규화 하고 학습용 데이터를 생성한다.

생성된 학습 데이터는 아래와 같은 형태다.

1
2
3
4
5
6
7
8
9
10
11
12
0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60
0	0.780367	0.624690	0.598909	0.559742	0.419435	0.454636	0.433317	0.390183	0.158651	0.132871	0.178483	0.085275	0.062469	0.044125	0.040654	0.031730	0.053049	0.111056	0.101636	0.087754	0.115518	0.124442	0.109073	0.086267	0.152206	0.257313	0.288547	0.303917	0.233515	0.200793	0.274510	0.294118	0.235294	0.235294	0.215686	0.215686	0.215686	0.196078	0.058824	0.078431	0.000000	0.019608	0.019608	0.019608	0.019608	0.039216	0.019608	0.098039	0.098039	0.117647	0.117647	0.137255	0.117647	0.176471	0.196078	0.392157	0.431373	0.470588	0.529412	0.529412	0
1	0.945708	0.868666	0.739917	0.754912	0.725440	0.703723	0.612203	0.594105	0.613754	0.617890	0.556360	0.573423	0.528438	0.531541	0.517063	0.539814	0.533609	0.492761	0.474664	0.433816	0.444157	0.507756	0.417787	0.407963	0.398656	0.395553	0.345915	0.305584	0.326267	0.316960	0.052632	0.078947	0.052632	0.078947	0.078947	0.078947	0.000000	0.052632	0.052632	0.000000	0.078947	0.052632	0.105263	0.131579	0.078947	0.078947	0.052632	0.052632	0.078947	0.052632	0.000000	0.026316	0.026316	0.000000	0.078947	0.078947	0.078947	0.052632	0.052632	0.052632	0
2	0.920393	0.962162	1.000000	0.951351	0.954791	0.911057	0.958231	0.939066	0.948403	0.917445	0.929730	0.888943	0.868796	0.854545	0.835381	0.815725	0.877150	0.858968	0.905160	0.886978	0.819165	0.782801	0.747912	0.753317	0.688452	0.661916	0.646683	0.630958	0.640295	0.624079	0.454545	0.363636	0.272727	0.272727	0.272727	0.363636	0.454545	0.454545	0.363636	0.454545	0.454545	0.454545	0.545455	0.454545	0.545455	0.636364	0.727273	0.818182	0.818182	0.818182	0.909091	0.636364	0.545455	0.545455	0.636364	0.636364	0.454545	0.454545	0.454545	0.454545	0
3	0.417309	0.276778	0.316195	0.395887	0.402742	0.413025	0.444730	0.381320	0.386461	0.343616	0.301628	0.303342	0.345330	0.377035	0.478149	0.371037	0.161954	0.143102	0.216795	0.216795	0.239075	0.248500	0.316195	0.311054	0.450728	0.508141	0.462725	0.307626	0.337618	0.550985	0.441176	0.441176	0.441176	0.411765	0.411765	0.352941	0.411765	0.411765	0.441176	0.411765	0.411765	0.382353	0.441176	0.441176	0.411765	0.411765	0.382353	0.382353	0.382353	0.382353	0.382353	0.441176	0.441176	0.500000	0.500000	0.500000	0.500000	0.529412	0.500000	0.470588	0
4	0.136275	0.070651	0.032393	0.021223	0.010612	0.007819	0.000000	0.013404	0.013963	0.024574	0.014800	0.012846	0.057526	0.068696	0.046077	0.107791	0.141860	0.160570	0.128456	0.106395	0.109187	0.096342	0.117565	0.133203	0.089081	0.076515	0.102765	0.101648	0.104719	0.120916	0.611111	0.611111	0.611111	0.611111	0.555556	0.555556	0.500000	0.555556	0.611111	0.555556	0.500000	0.500000	0.555556	0.444444	0.500000	0.500000	0.500000	0.444444	0.500000	0.444444	0.500000	0.444444	0.500000	0.500000	0.500000	0.555556	0.555556	0.444444	0.500000	0.444444	0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
905	0.531307	0.745928	0.805646	0.934491	0.959464	0.934491	0.899385	0.917119	0.832429	0.835324	0.669924	0.801665	0.785378	0.898299	1.000000	0.871516	0.674267	0.777416	0.802027	0.812161	0.836772	0.728194	0.742309	0.589215	0.562432	0.553384	0.584872	0.612740	0.591748	0.548317	0.089172	0.085987	0.108280	0.111465	0.124204	0.101911	0.073248	0.066879	0.063694	0.073248	0.073248	0.076433	0.076433	0.066879	0.073248	0.085987	0.073248	0.082803	0.079618	0.092357	0.089172	0.060510	0.076433	0.073248	0.076433	0.085987	0.082803	0.082803	0.073248	0.070064	1
906	0.127696	0.094170	0.159086	0.172966	0.100577	0.061499	0.053171	0.076233	0.065129	0.071108	0.019646	0.000427	0.000000	0.012599	0.013239	0.009823	0.026479	0.056161	0.064916	0.041854	0.023703	0.007047	0.045270	0.031177	0.035234	0.033953	0.027333	0.055947	0.051036	0.049327	0.550725	0.528986	0.463768	0.478261	0.442029	0.456522	0.492754	0.478261	0.456522	0.413043	0.442029	0.398551	0.384058	0.355072	0.347826	0.347826	0.326087	0.326087	0.347826	0.311594	0.347826	0.318841	0.326087	0.246377	0.246377	0.217391	0.217391	0.173913	0.239130	0.260870	0
907	0.125000	0.321429	0.261905	0.251253	0.224311	0.252506	0.283521	0.234649	0.218985	0.176065	0.232143	0.283835	0.479010	0.501566	0.528509	0.595238	0.591792	0.571429	0.583020	0.604323	0.618108	0.625000	0.623120	0.604010	0.604950	0.617481	0.544799	0.536967	0.543860	0.475564	0.678161	0.689655	0.689655	0.712644	0.729885	0.747126	0.770115	0.775862	0.781609	0.787356	0.793103	0.833333	0.816092	0.816092	0.810345	0.781609	0.793103	0.827586	0.856322	0.833333	0.844828	0.850575	0.833333	0.879310	0.844828	0.827586	0.827586	0.798851	0.804598	0.816092	0
908	0.401929	0.343822	0.227147	0.194993	0.229904	0.238401	0.192007	0.112770	0.126321	0.105880	0.097382	0.110703	0.162150	0.121727	0.081994	0.065687	0.067754	0.063390	0.074874	0.087046	0.055581	0.107717	0.061323	0.055811	0.041801	0.035599	0.000000	0.036059	0.058567	0.075333	0.979275	0.994819	0.953368	0.932642	0.958549	0.968912	0.932642	0.911917	0.948187	0.979275	1.000000	0.994819	0.994819	0.958549	0.953368	0.927461	0.911917	0.932642	0.953368	0.948187	0.979275	0.958549	0.979275	0.937824	0.932642	0.932642	0.979275	0.984456	0.974093	0.958549	0
909	0.018349	0.033276	0.045872	0.023636	0.012284	0.027678	0.052247	0.081947	0.096564	0.081014	0.074016	0.088944	0.080858	0.043228	0.027523	0.046494	0.050381	0.050536	0.077437	0.067797	0.062510	0.029544	0.009641	0.044006	0.046649	0.061888	0.075260	0.088167	0.058311	0.051625	0.000000	0.067797	0.067797	0.322034	0.372881	0.474576	0.474576	0.457627	0.576271	0.508475	0.508475	0.491525	0.593220	0.694915	0.661017	0.745763	0.813559	0.779661	0.847458	0.881356	0.949153	1.000000	0.966102	0.983051	0.966102	0.881356	0.898305	0.915254	0.932203	0.966102	0

한 row당 하루의 장 흐름 데이터이며

col 0~29은 외국인 순 거래량 분봉 데이터, 30 ~ 59은 선물 지수 분봉 데이터, 마지막 60은 1%이상 상승했는지를 나타내는 Label이다.

모델 생성

데이터는 준비되었으니 준비된 데이터로 학습을 진행한다.

학습 이전에 학습용 데이터와 테스트용 데이터를 7:3 비율로 나눈다.

1
2
3
4
5
6
7
from sklearn.model_selection import train_test_split
train = pd.read_csv('data/train_with_index.csv')

x = train.iloc[:, :60]
y = train['60']

train_x, test_x, train_y, test_y = train_test_split(x, y, test_size = 0.3, random_state=123)

학습에 사용할 라이브러리는 AutoKeras이다.

AutoKeras의 사용법은 간단하다. 학습시킬 데이터의 형태에 맞는 클래스를 선택해서 최대 반복 횟수와 epochs만 지정해주면 학습을 반복하면서 가장 성능이 좋은 모델을 찾아낸다.

만약 더이상 성능이 개선될 여지가 없으면 조기 종료된다.

1
2
3
4
5
6
7
8
9
10
import autokeras as ak

clf = ak.StructuredDataClassifier(
    overwrite=True, max_trials=300
)

clf.fit(
    x=train_x, y=train_y,
    epochs=20
)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
Trial 54 Complete [00h 00m 07s]
val_accuracy: 0.8560000061988831

Best val_accuracy So Far: 0.9120000004768372
Total elapsed time: 00h 05m 44s
INFO:tensorflow:Oracle triggered exit
Epoch 1/20
20/20 [==============================] - 1s 3ms/step - loss: 0.4540 - accuracy: 0.7622
Epoch 2/20
20/20 [==============================] - 0s 4ms/step - loss: 0.3211 - accuracy: 0.8421
Epoch 3/20
20/20 [==============================] - 0s 4ms/step - loss: 0.2995 - accuracy: 0.8523
Epoch 4/20
20/20 [==============================] - 0s 3ms/step - loss: 0.2896 - accuracy: 0.8717
Epoch 5/20
20/20 [==============================] - 0s 3ms/step - loss: 0.2848 - accuracy: 0.8792
Epoch 6/20
20/20 [==============================] - 0s 4ms/step - loss: 0.2821 - accuracy: 0.8736
Epoch 7/20
20/20 [==============================] - 0s 3ms/step - loss: 0.2740 - accuracy: 0.8794
Epoch 8/20
20/20 [==============================] - 0s 4ms/step - loss: 0.2737 - accuracy: 0.8708
Epoch 9/20
20/20 [==============================] - 0s 3ms/step - loss: 0.2689 - accuracy: 0.8691
Epoch 10/20
20/20 [==============================] - 0s 3ms/step - loss: 0.2693 - accuracy: 0.8718
Epoch 11/20
20/20 [==============================] - 0s 4ms/step - loss: 0.2643 - accuracy: 0.8721
Epoch 12/20
20/20 [==============================] - 0s 5ms/step - loss: 0.2680 - accuracy: 0.8651
Epoch 13/20
20/20 [==============================] - 0s 5ms/step - loss: 0.2601 - accuracy: 0.8693
Epoch 14/20
20/20 [==============================] - 0s 4ms/step - loss: 0.2622 - accuracy: 0.8711
Epoch 15/20
20/20 [==============================] - 0s 5ms/step - loss: 0.2537 - accuracy: 0.8711
Epoch 16/20
20/20 [==============================] - 0s 5ms/step - loss: 0.2589 - accuracy: 0.8696
Epoch 17/20
20/20 [==============================] - 0s 4ms/step - loss: 0.2529 - accuracy: 0.8661
Epoch 18/20
20/20 [==============================] - 0s 4ms/step - loss: 0.2512 - accuracy: 0.8718
Epoch 19/20
20/20 [==============================] - 0s 5ms/step - loss: 0.2498 - accuracy: 0.8783
Epoch 20/20
20/20 [==============================] - 0s 4ms/step - loss: 0.2458 - accuracy: 0.8821
INFO:tensorflow:Assets written to: ./structured_data_classifier/best_model/assets

54번의 반복후에 91%의 정확도를 가진 모델이 생성되었다.

평가

내부적으로 학습 데이터를 나누어 (20%) 검증에 사용하지만 따로 분리해 둔 테스트용 데이터로 성능을 다시 테스트 해본다.

1
2
3
4
5
6
7
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report

pre = clf.predict(test_x)

print(classification_report(test_y, pre))
print(confusion_matrix(test_y, pre))

1
2
3
4
5
6
7
8
9
10
11
               precision    recall  f1-score   support

           0       0.90      0.93      0.91       233
           1       0.47      0.38      0.42        40

    accuracy                           0.85       273
   macro avg       0.68      0.65      0.66       273
weighted avg       0.83      0.85      0.84       273

[[216  17]
 [ 25  15]]

평균 정확도는 85%이지만 자세히 살펴보면 Positve을 예측하는 정도, 즉 1% 이상 오르는지에 대한 예측 성능은 낮다.

Precision, Recall, F1-Score 전부 0.5 이하의 점수가 나온다.

즉 지금 데이터로는 장 마감시 지수 예측을 거의 못한다는 뜻이다.